The children are transformations of the parent Some functions will shift upward or downward, open wider or more narrow, boldly rotate 180 degrees, or a combination of the above Learn why a parabola opens wider, opens more narrow, orTap for more steps Use the form a x 2 b x c a x 2 b x c, to find the values of a a, b b, and c c a = − 1, b = − 4, c = − 3 a = 1, b = 4, c = 3 Consider the vertex form of a parabola a ( x d) 2 e a ( x d) 2 e Substitute the values of a a and b b into the formula d = b 2 a d = b 2 aY = x 2 3x 13;
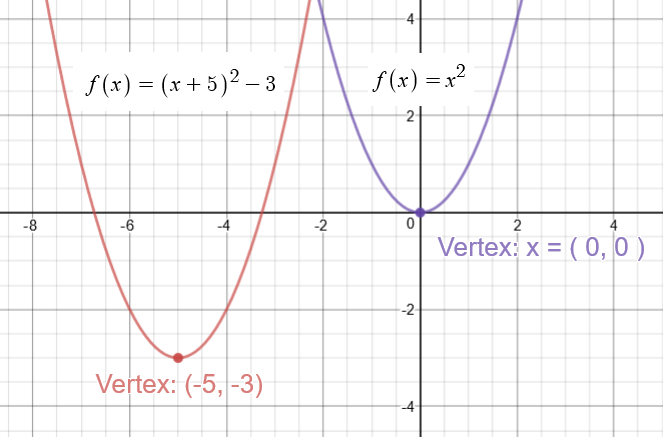
How To Graph A Parabola Y X 5 2 3 Socratic
Y=x^2+3 parabola
Y=x^2+3 parabola-Complete the square for x 2 − 3 x 2 3 Tap for more steps Use the form a x 2 b x c a x 2 b x c, to find the values of a a, b b, and c c a = 1, b = 0, c = − 3 a = 1, b = 0, c = 3 Consider the vertex form of a parabola a ( x d) 2 e a ( x d) 2 e∞) все действительные числа 2 Область значений y ∈ 0;



Q Tbn And9gcrbi9blo Wofvbzwqyztuiacedgeo1l24bjehodcy52fa23rbjt Usqp Cau
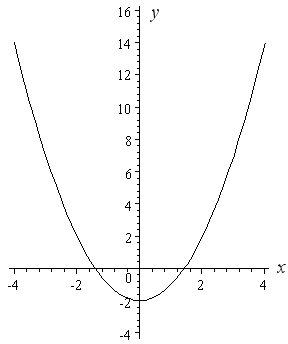
This should do import matplotlibpyplot as plt import numpy as np # create 1000 equally spaced points between 10 and 10 x = nplinspace (10, 10, 1000) # calculate the y value for each element of the x vector y = x**2 2*x 2 fig, ax = pltsubplots () axplot (x, y) This is your approach with as few changes as possible to make it workThe vertex is the minimum point in a parabola that opens upward In a parabola that opens downward, the vertex is the maximum point We can graph a parabola with a different vertex Observe the graph of y = x 2 3 Graph of y = x 2 3 The graph is shifted up 3 units from the graph of y = x 2, and the vertex is (0, 3) Observe the graph of y = x 2 3$\begingroup$ After this substitution (and pulling the constant factor out) the integrand is $\sec^3 \theta$, not $\sec^4 \theta$this significantly changes the mechanics of evaluating the integral
Graph the parabola y = x2 3 by plotting any three points on the parabola Move the key points on the graph to create the parabola Provide your answer below 10 < Previous Next A chord of the parabola y = x 2 2 5 = joins the point with the abscissas x 1 x 1 , x 2 = 3 Then the equation of the tangent to the parabola parallel to the chord is (A) 2x y 5/4 = 0 (B) 2x – y 2 = 0 2x – y 1 = 0 (D) 2x y 1 = 0 #y=x^2# is the Parent Function for a quadratic equation The graph of #y=x^2# is useful in understanding the behavior of the function given #color(red)(y = 4x^2# Since, the sign of the #x^2# term is positive , the parabola opens up and we have a Minimum point at the Vertex
In y = x^2 we're done, that is the y value In y = (x2)^2, after we square, we are done, that is the y value In y = (x2)^2 3, after we square, we still need to subtract 3 from the number, that moves us down 3 The vertex of y=x^2 is the point (0,0) TheY = ax 2 bx c or x = ay 2 by c 2 Geometric A parabola is In the equation (y 1) 2 = x, the "plus 1" in brackets has the effect of moving our rotated parabola down one unit Example 8 (y − 3) 2 = x Using similar reasoning to the above example, the "minus 3" in brackets has the effect of moving the rotated parabola up 3 units Finally we are ready to answer the question posed by Nuaja Example 9 y 2 = x − 2



Intro To Quadratic Graphs Key Features Of Parabolas Expii




The Distance Between The Vertex Of The Parabola Y X 2 4x
Consider the parabola y = x 2 Since all parabolas are similar, this simple case represents all others Construction and definitions The point E is an arbitrary point on the parabola The focus is F, the vertex is A (the origin), and the line FA is the axis of symmetry The line EC is parallel to the axis of symmetry and intersects the x axis at DCOMEDK 05 The shortest distance from the point (3, 0) to the parabola y = x2 is (A) √3 (B) 3 5 (D) √5 Check Answer and Solution for aboveI have an equation right here it's a second degree equation it's a quadratic and I know it's graph is going to be a parabola this was a review that means it looks something like this or it looks something like that because the coefficient on the x squared term here is positive and it's going to be an upwardopening parabola and I am curious about the vertex of this parabola and if I have



Parabolas




Is The Parabola Described By Y 2x 2 Wider Or Narrower Than The Parabola Described By Y X 2 Socratic
See the answer Show transcribed image text Expert Answer 100% (1 rating) Previous question Next question0 votes 1 answer If the area bounded by the parabola y^2 = 4ax and the line y y = x 2, where x ≠ 0 Here are a few quadratic functions y = x 2 5;



Content Focus Directrix Definition Of The Parabola




Quadratic Function
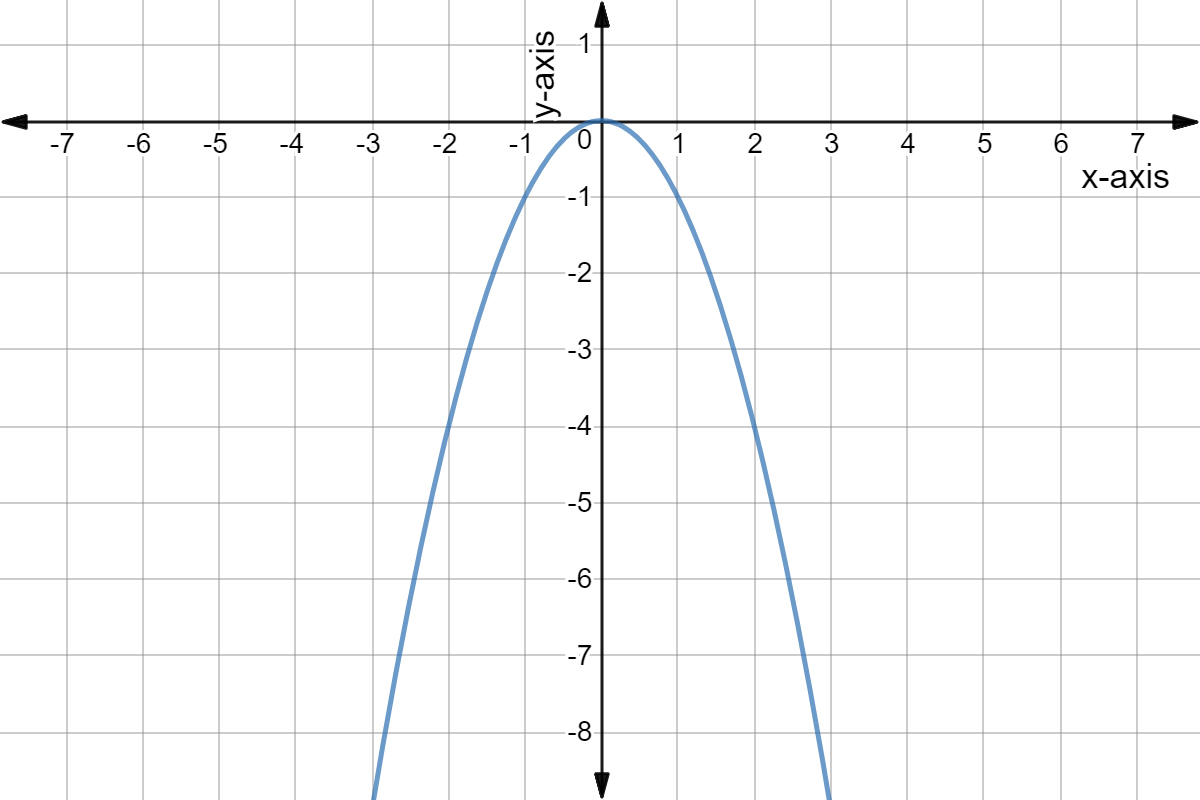
One formula works when the parabola's equation is in vertex form and the other works when the parabola's equation is in standard form Standard Form If your equation is in the standard form $$ y = ax^2 bx c $$ , then the formula for the axis of symmetry is $ \red{ \boxed{ x∞) все неотрицательные действительные числа 3 Функция убывает при x < 0How to Graph a Parabola with no xintercepts y = x^2 2 Watch later Share Copy link Info Shopping Tap to unmute If playback doesn't begin shortly, try restarting your device



Graphing Quadratic Functions



The Parabola Y X 2 C Is To Be Tangent To The Line X Y What Is The Value Of C Quora
The reference parabola ( y = x 2) is drawn in transparent light gray, and the transformed parabola which is vertically scaled by a factor of 3 ( y = 3x 2) is drawn in black What follows is an animation that presents many vertical scalings for our reference parabolaFind an answer to your question "The parabola y=x^2 is scaled vertically by a factor of 2/3 what's the equation of the new parabola also i need this fast i'm on time " in 📘 Mathematics if you're in doubt about the correctness of the answers or there's no answer, then try to use the smart search and find answers to the similar questions Column A A1 Make it X place a negative number, like 10 or100 A3 next number in sequence, like 9 or 99 select the two numbers, and drag down until your at 10 or 100 B Make it Y B2 put in formula, =A^23 Drag down



Quadratics Graphing Parabolas Sparknotes



How Do I Convert The Equation F X X 2 2x 3 To Vertex Form Socratic
Notice, Solving the equation of straight line y=kx1 & equation of the parabola y=x^23 kx1=x^23\iff x^2kx4=0 Now, the line will touch the parabola if both real roots of the above Notice, Solving the equation of straight line y = k x − 1 & equation of the parabola y = x 2 3 k x − 1 = x 2 3 x 2 − k x 4 = 0 Now, the line will touch the parabola if both real roots of the aboveSelect any horizontal segment to be the base Take the distance between the base and the vertex to be the height of the parabolic area The area is ( 2 / 3 ) b h If the sides are linear, the area is ( 1 / 2 ) b h If the sides are cubic, the arQuestion The Parabola Y = X^2 3x Has It's Focus At The Point (b, C) Where This problem has been solved!




The Graph Of The Quadratic Function Y X2 Is Shown Below If This Parabola Is Reflected About The Brainly Com



Graphing Quadratic Functions
It is a standard horizontal parabola, the formula being y^2 = ax The focus point is formula a = 4p I know that Math Choose the three true statements about the graph of the quadratic function y = x2 − 3x − 4 Options A) The graph is a parabola with a minimum point B) The graph is a parabola with a maximum point The area (in sq units) bounded by the parabola y = x^2 1, the tangent at the point (2, 3) to it and the yaxis asked in Mathematics by Simrank (721k points) jee mains 19;The equation, \( y = x ^ { 2 } 3 \) represents a parabola that intersects yaxis at the point \( Q \) lf \( P \) is apoiat on the parabola having coordinates \( ( 2 , k ) , \) what is the distance between the point P and the point \( Q \) \( ( \mathbf { A } ) \) (B) 7 2\( \sqrt { 5 } \) \( ( D ) \quad 3 \sqrt { 3



Math Spoken Here Classes Quadratic Equations 3
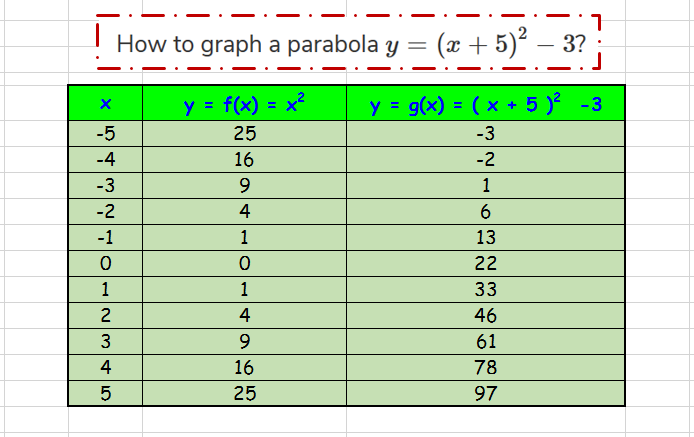



How To Graph A Parabola Y X 5 2 3 Socratic
Y = x 2 5x 3;Parábola con ecuación y = x2 Autor Hébert Ariel Nevárez González Tema Parábola Este applet permite observar el comportamiento de la gráfica de la parábola al variar los componentes de la ecuación base y = x2 You have conic y = x 2, so matrix M is given by π 4 0 0 0 1) x 2 − 2 x y y 2 − x 2 − y 2 = 0 Your result is corect This is the plot in geogebraorg where t ∈ R You are rotating each point of the parabola, and hence X ( t) Y ( t) = 2 2 1 − 1 1



Quadratic Function Parabola



Parabolas
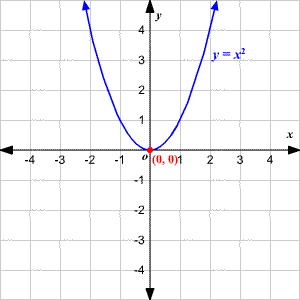
In the figure, the vertex of the graph of y=x 2 is (0,0) and the line of symmetry is x = 0 Definition Parabola 1Algebric A Parabola is the graph of a quadratic relation of either form where a ≠ 0; Consider a parabola y = x^2 Answer the following questions and fill in your responses in the corresponding boxes on the answer sheets (1) the line that goes through the point (0, 3/2) and is orthogonal to a tangent line to the part of parabola y = x^2 with x > 0 is y = Ax 3The Parabola Y = X^2 3x Has It's Focus At The Point (b, C) Where;



Instructional Unit The Parabola Day 4 And 5



Math Spoken Here Classes Quadratic Equations 3
Get an answer for 'Find the equation of both lines that pass through the point (2, 3) and are tangent to the parabola y = x^2 x' and findY=3x^2 Calculadora para parábolas Symbolab Calculadora gratuita para parábolas Calcular los focos de una parábola, sus vértices, ejes y su directriz paso por paso This website uses cookiesTURNING POINT The formula to find the x value of the turning point of the parabola is x = –b/2a



Shift The Graph F The Parabola Y X 2 By 3 Units To The Left Then Reflect The Graph Obtained On The X Axis And Then Shift It 4 Units Up What Is The Equation



How To Draw Y 2 X 2
When you solve the quadratic equation y = x 2 – 6x 8 = 0 by factorization or by formula, x = 2 or 4 These are the 2 roots of the equation What do you notice about these roots and the points at which the parabola crosses the xaxis?Свойства параболы y=x² 1 Область определения x ∈ ( − ∞;Examples (y2)=3(x5)^2 foci\3x^22x5y6=0 vertices\x=y^2 axis\(y3)^2=8(x5) directrix\(x3)^2=(y1) parabolaequationcalculator y=3x^{2}



1




Scaling Reflecting Parabolas Video Khan Academy
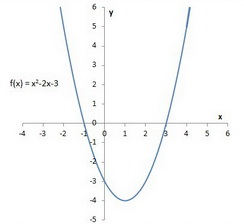
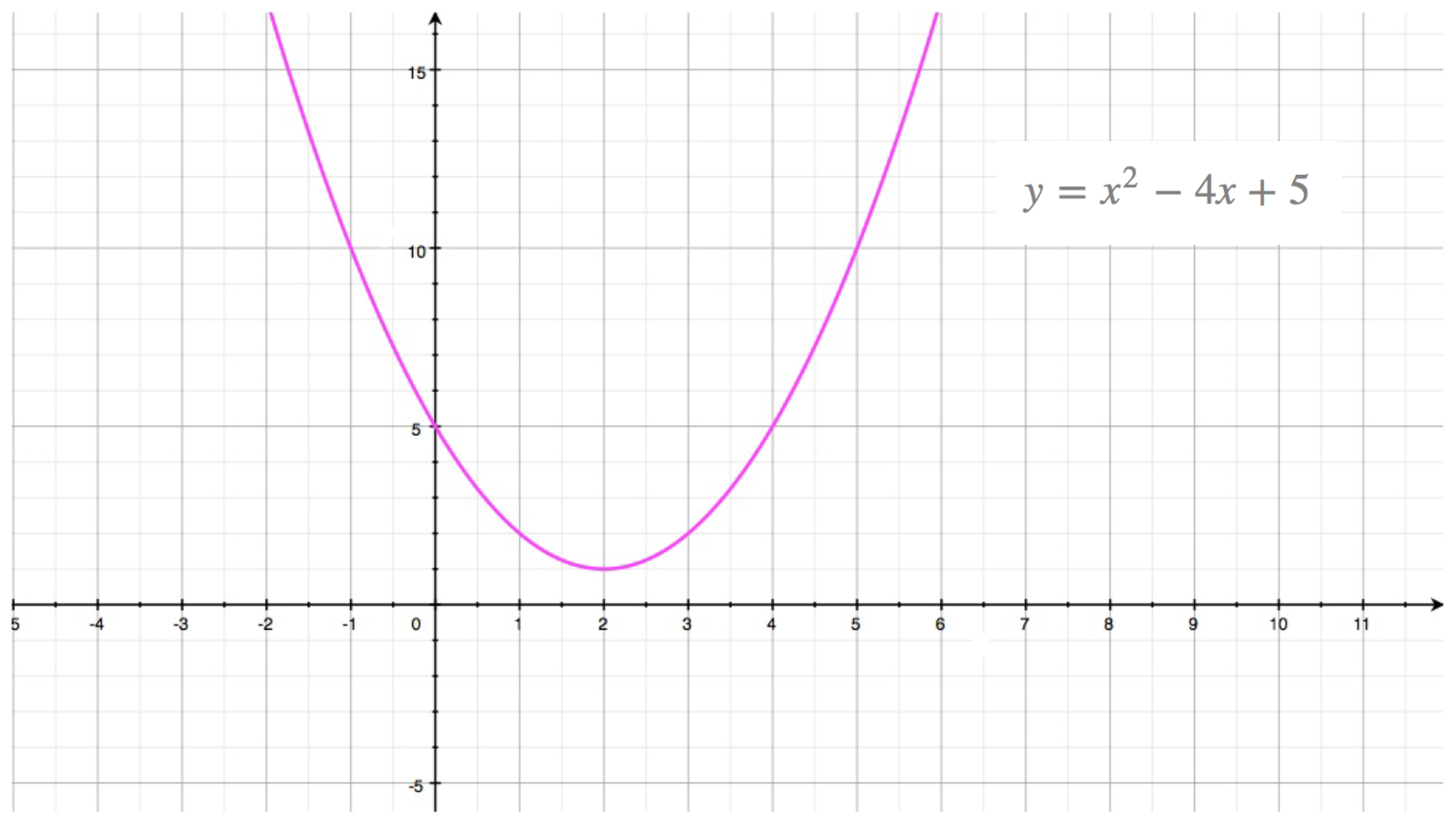
Mathy=x^2bxc/math What we are really looking for is a value for mathb/math and mathc/math Once we can find those two values, we can simply plug them back into mathy=x^2bxc/math to get the equation of the parabola Let's start Find the area of the region bounded by the parabola y = 3x^2, the tangent line to this parabola at (1, 3), and the xaxis Calculus Centers of Mass Find the centroid of the region in the first quadrant bounded by the xaxis, the parabola y^2 = 2x, and the line x y = 4{eq}\displaystyle y = x^2 2x 3 {/eq} Parabola In geometry, the parabola is defined as the curve or graph equivalent to the graph of {eq}{x^2}{/eq} but the equation of the parabola depends on
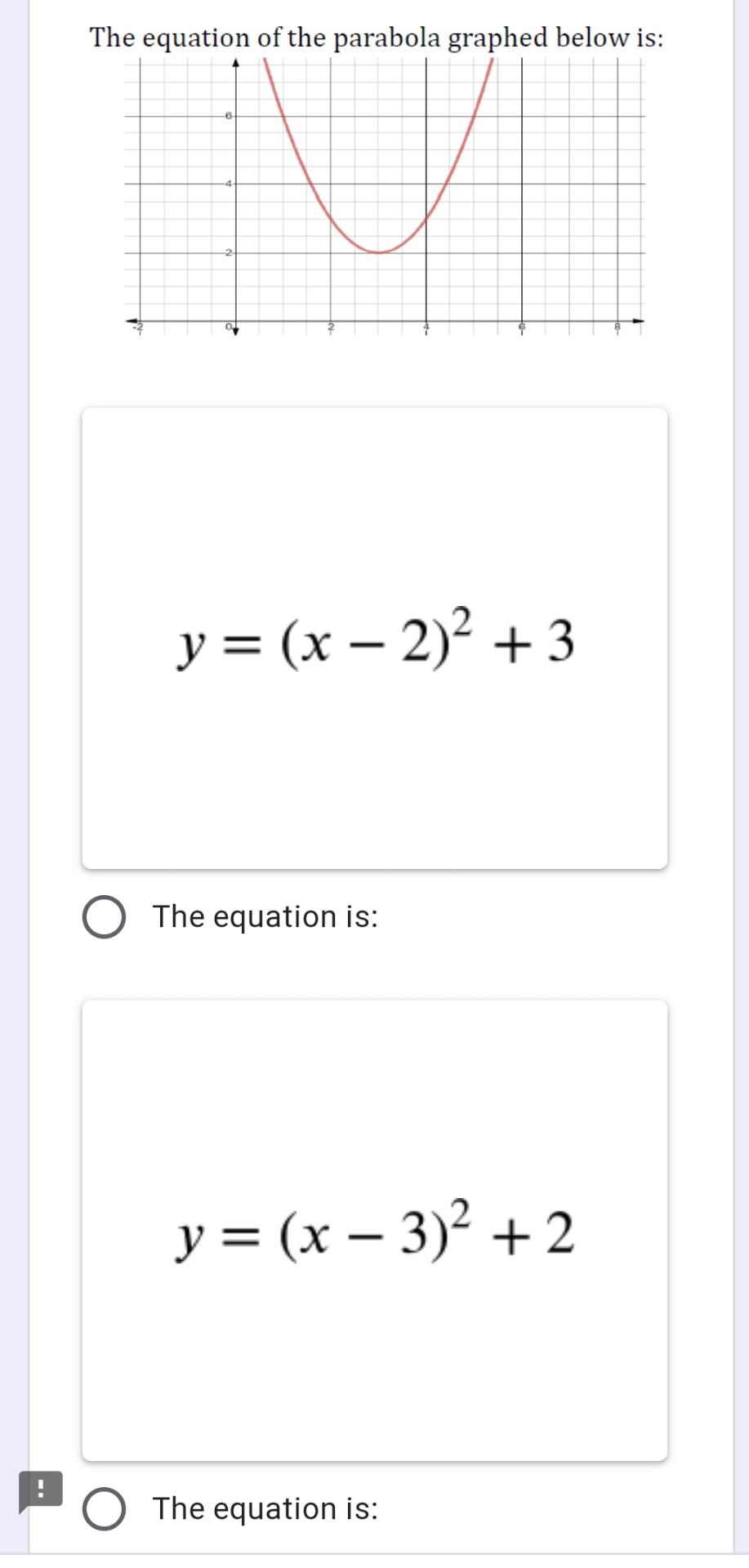



Solved The Equation Of The Parabola Graphed Below Is Y Chegg Com




Shifting Parabolas Video Khan Academy
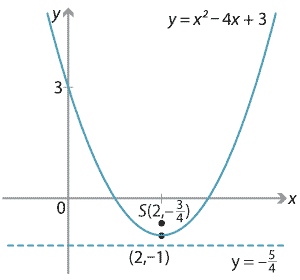
Example 1 Graph by plotting points y = x2 − 2x − 3 Solution In this example, choose the x values {−2, −1, 0, 1, 2, 3, 4} and calculate the corresponding y values Plot these points and determine the shape of the graph Answer When graphing, we want to include certain special points in the graphFind the equation of both lines that pass through the point (2, 3) and are tangent to the parabola y = x^2 x 3 Educator answers Math Latest answer posted at AMY=x^24x3 can be factored as y=(x1)(x3) so the vertex of the parabola is at x=2, midway between 1 and 3 To get the left side of the parabola you need to force the xcoordinate to be 2 or less That is you want x to be 2 minus something that is positive, or at least 2 minus something that is never negative Thus let x=2t^2 and whatever



Parabola Parent Function Mathbitsnotebook A1 Ccss Math



How To Do You Graph Y 2x 2 X 3 By Plotting Points Socratic
Graphing Parabolas Part 3 Graphing Parabolas Part 4 Graphing Recap Graphing by Completing the Square Intro Graphing by Completing the Square How Graphing by Completing the Square Freaky Things That Can Happen Making the Connection Between Graphing and Standard Equation of Parabola The simplest equation of a parabola is y 2 = x when the directrix is parallel to the yaxis In general, if the directrix is parallel to the yaxis in the standard equation of a parabola is given as y2 = 4axThe parabola defined by \y = x^22x3\ has \(y\)intercept at \\begin{pmatrix}0,3\end{pmatrix}\ Where \(3\) is the only term without an \(x\) in the parabola's equation This can be seen on this parabola's graph We can see that \(y=x^22x3\) cuts the \(y\)axis at the point \(\begin{pmatrix}0,3 \end{pmatrix}\)



How To Draw Y 2 X 2




What Is The Axis Of Symmetry For The Parabola Y Chegg Com
Our quadratic equation is {eq}y = x^2 2x 3 {/eq} Step 1 First we need to find the vertex of our parabola The vertex is given by the points {eq}\left(\dfrac{b}{2a}, f(\dfrac{b}{2a})\rightEquation of the parabola $$$ y=2 x^{2} x 3 $$$ Vertex form $$$ y=2 \left(x \frac{1}{4}\right)^{2} \frac{23}{8} $$$ No intercept form Vertex $$$ \left(\frac{1}{4},\frac{23}{8}\right) $$$ Focus $$$ \left(\frac{1}{4},3\right) $$$ Eccentricity $$$ 1 $$$ Directrix $$$ y=\frac{11}{4} $$$ Latus rectum $$$ y=3 $$$A line passing through the point of intersection of x y = 4 and x − y = 2 makes an angle tan − 1 (4 3 ) with the xaxis It intersects the parabola y 2 = 4 (x − 3) at points (x 1 , y 1 ) and (x 2 , y 2 ) respectively Then ∣ x 1 − x 2 ∣ is equal to




Quadratic Function




Solved 4 For The Parabola Y X 2 3 A Does It H Chegg Com




Find The Coordinates Of A Point On The Parabola Y X 2 7x 2 Which
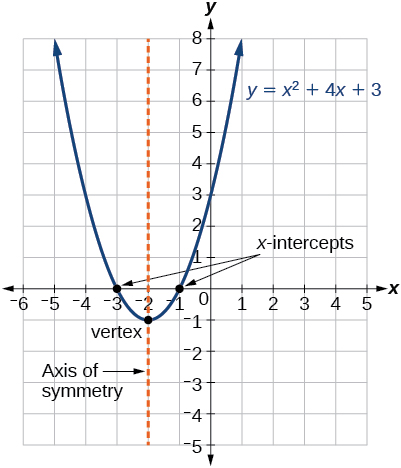



5 1 Quadratic Functions Mathematics Libretexts
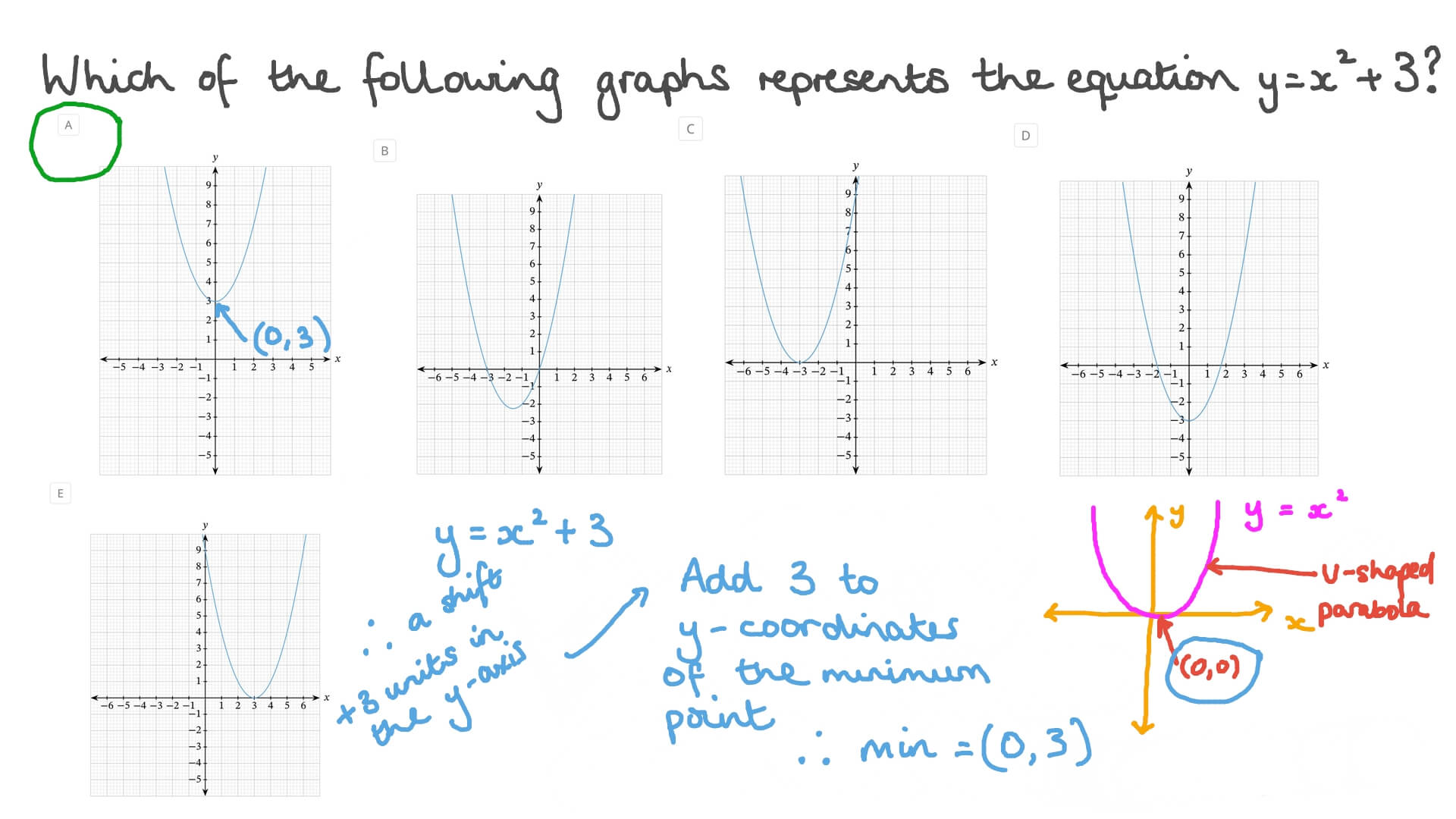



Question Video Identifying Graphs Of Quadratic Equations In Vertex Form Nagwa




The Graph Of The Parabola Y 2 X 3 2 4 Has A Vertex Of 3 4 If This Parabola Is Shifted 5units To Brainly Com




Understand How The Graph Of A Parabola Is Related To Its Quadratic Function College Algebra




Sketch A Graph Of The Parabola Y X 2 3 On The Same Graph Plot The Point 0 6 Note There Are Two Tangent Lines Of Y X 2 3



Q Tbn And9gcrbi9blo Wofvbzwqyztuiacedgeo1l24bjehodcy52fa23rbjt Usqp Cau




How Long Does A Firework Ppt Download
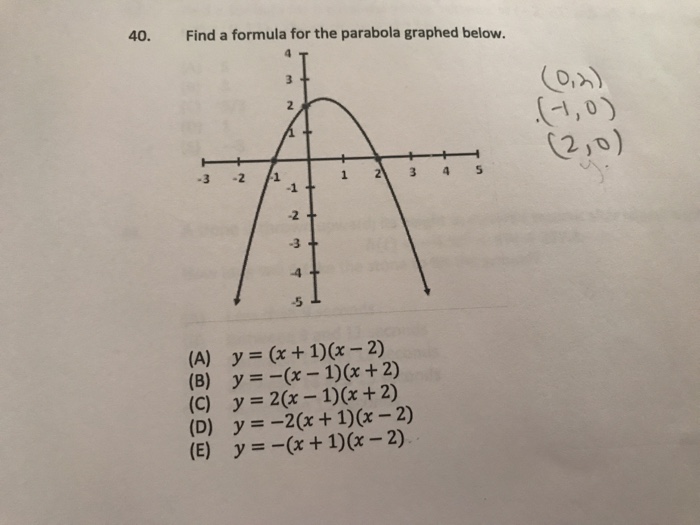



Solved 40 Find A Formula For The Parabola Graphed Below Chegg Com
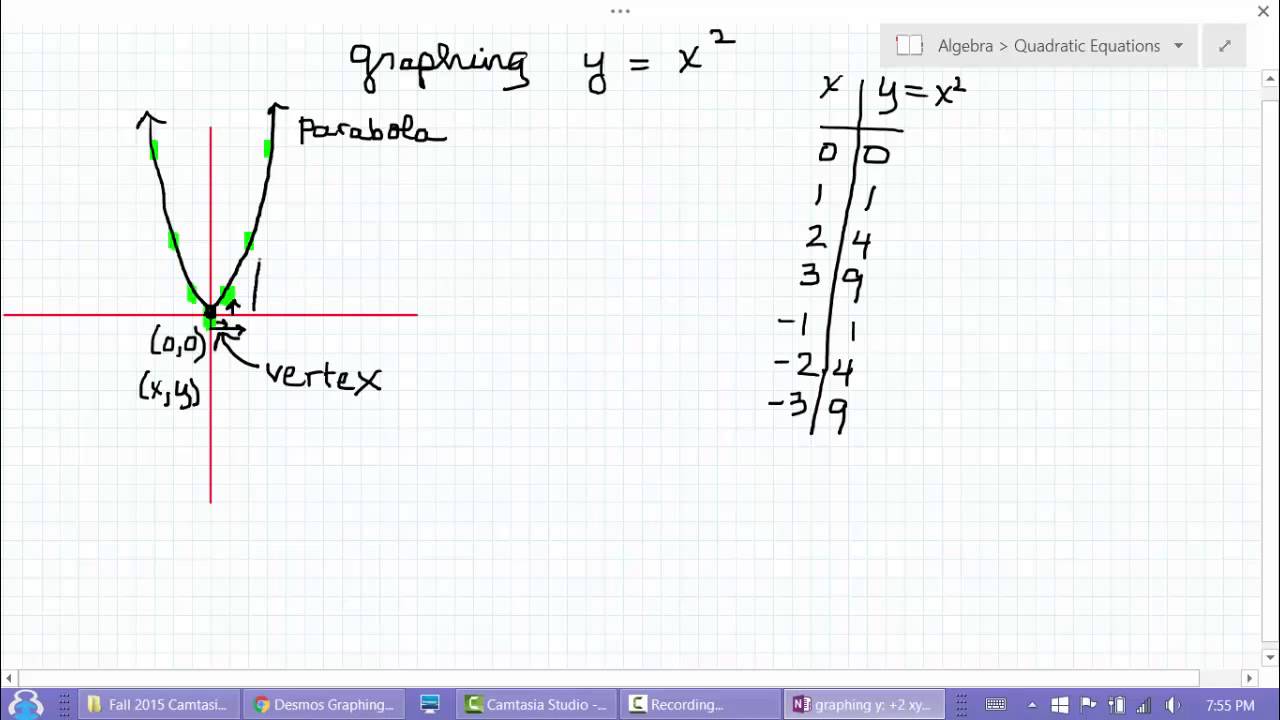



Graphing Basic Parabola Y X 2 Youtube



Math Spoken Here Classes Quadratic Equations 3
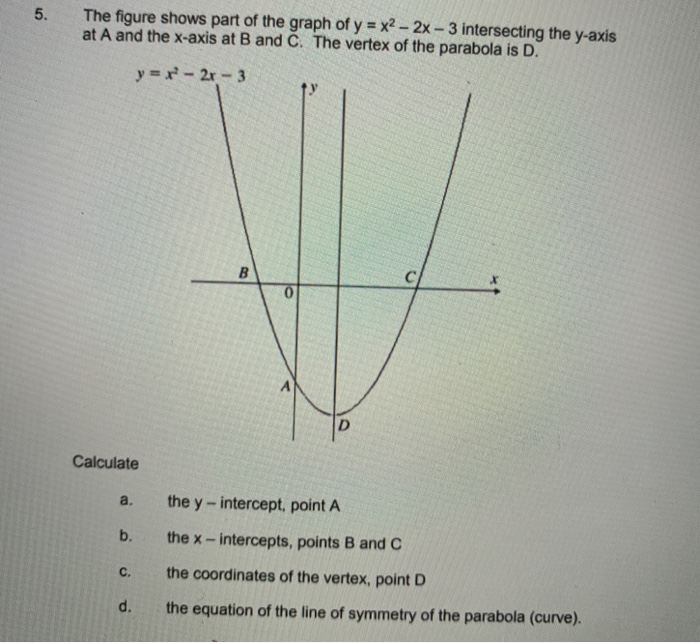



5 The Figure Shows Part Of The Graph Of Y X2 2x Chegg Com
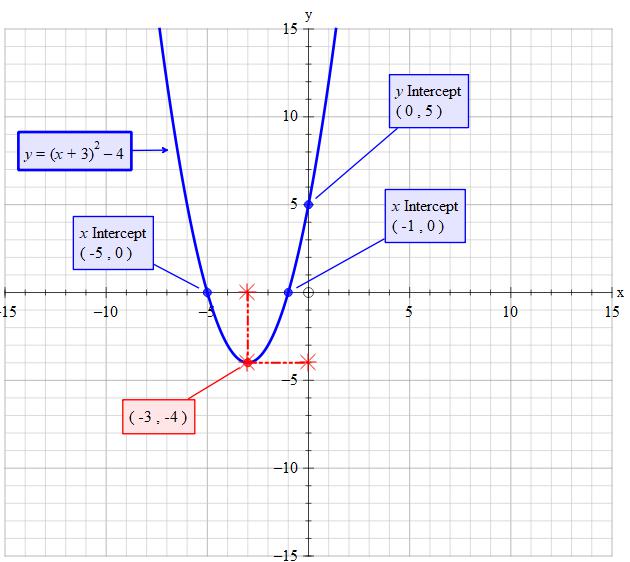



How Do You Find The Vertex And Intercepts For Y X 3 2 4 Socratic




Quadratic Function




Graphing Parabolas




How To Graph Y X 2 1 Youtube



Y X 2




Area Between Curves The Parabola Y 3 X 2 And Line Y X 1 Youtube




Vertical And Horizontal Transformations Read Algebra Ck 12 Foundation




How To Graph A Parabola Y X 5 2 3 Socratic




Plot A Graph For The Equation Y X 2 4x 1



The Graph Of Y Ax 2 Bx C Has A Minimum At 5 3 And Passes Through 4 0 How Do I Find The Values Of A B And C Quora




Graph Y X 2 1 Parabola Using A Table Of Values Video 3 Youtube



Quadratics Graphing Parabolas Sparknotes



How To Graph Y X 2 1 Youtube
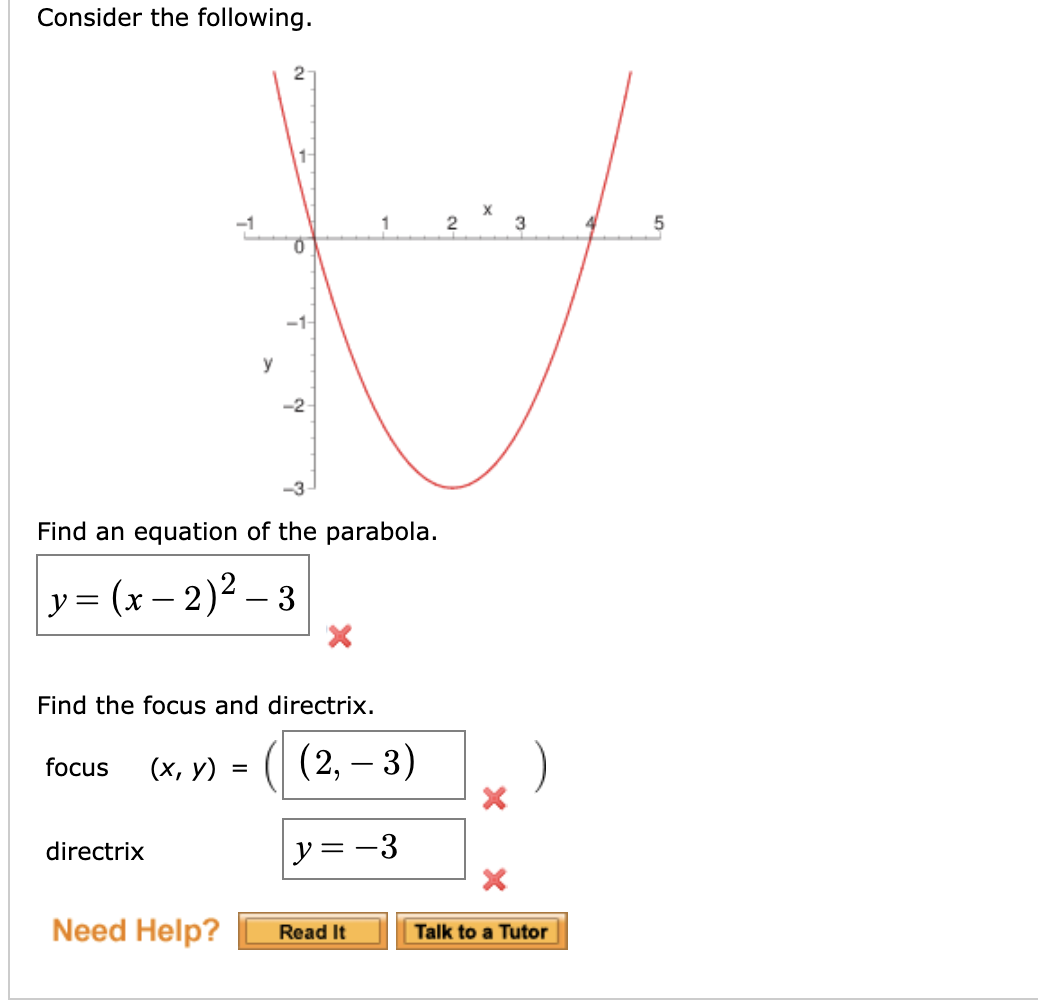



Consider The Following 3 5 1 Y 2 3 Find An Chegg Com
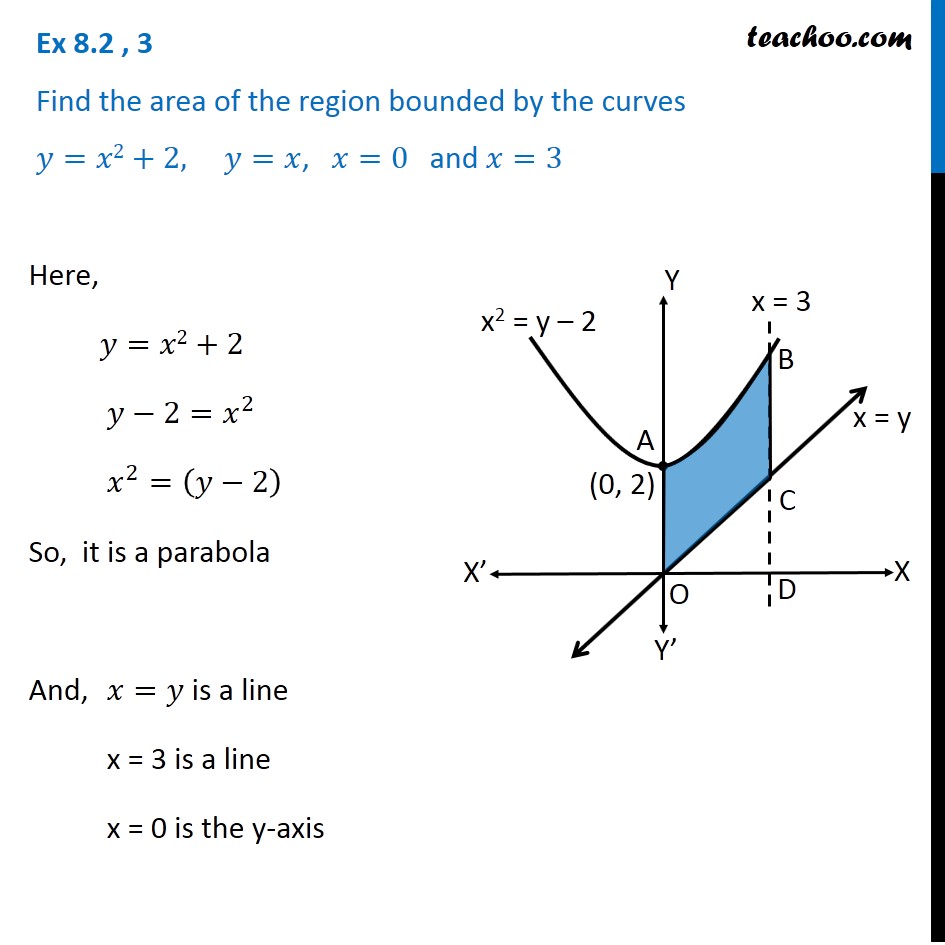



Ex 8 2 3 Find Area Bounded By Y X2 2 Y X X 0 3



How To Graph A Parabola Y X 5 2 3 Socratic



Search Q Y 3d1 X Tbm Isch



With Math Ax 2 Bx C Math Why Is The Math X Math Value Of The Vertex Of This Parabola Equal To Math B 2a Math Quora



Characteristics Of Parabolas College Algebra




Content Transformations Of The Parabola



Graphing Quadratic Functions




Find The Axis Of Symmetry 1 And The Vertex 2 Of A Parabola Ppt Download



Square And Cube Function Families Read Algebra Ck 12 Foundation



How To Graph A Parabola Of Y X 1 X 5 Mathskey Com




The Tangent To A Parabola Are X Y 0 And X Y 0 If The Focus Of The Parabola Is F 2 3 Then The Youtube




2 Use The Graph To Write An Equation For The Parabola 1 Point 1 Y 3x 2 2 Y X 2 9 3 Y X 2 3 4 Brainly Com



Solution Given The Equation Y X 2 7 Calculate The Corresponding Y Coordinates For X 3 1 0 1 3 Please Show All Of Your Work Plot Those Points And Graph The Equation
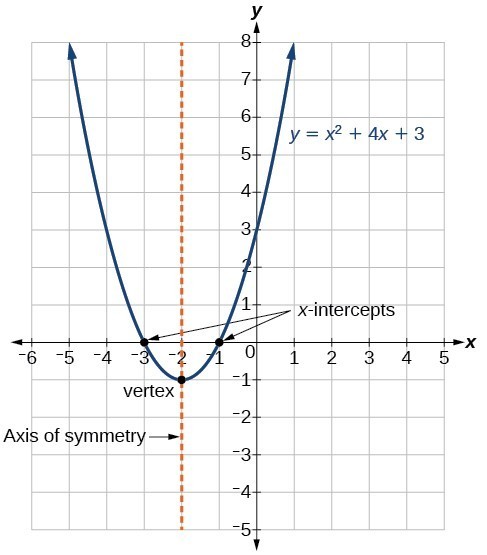



Understand How The Graph Of A Parabola Is Related To Its Quadratic Function College Algebra
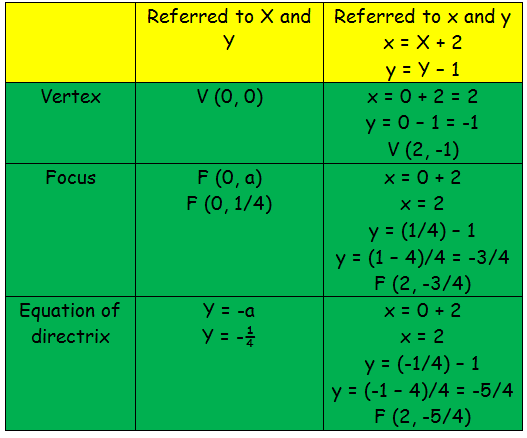



How To Find Focus Directrix And Vertex Of Parabola



Graphing Quadratic Functions



Graph Y X 7 X 3 Mathskey Com




Graphing Parabolas



Math Spoken Here Classes Quadratic Equations 3
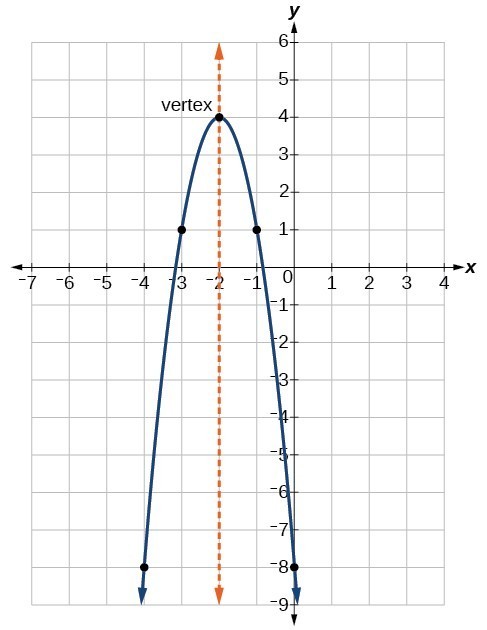



Understand How The Graph Of A Parabola Is Related To Its Quadratic Function College Algebra




The Parabola Below Is A Graph Of The Equation Y X 1 2 3 Which Point Will Satisfy The Brainly Com




Focus Of The Parabola Y 2 2 X 3 Is Youtube



Transformations




Content Transformations Of The Parabola




Graph Of Y X 2 The Equation For A Parabola Download Scientific Diagram



Solution How Do You Graph Y X 3 2 2



Exploration Of Parabolas




Consider A Parabola P That Is Congruent To Y X 2 Opens Upward And Has Vertex 0 0 Find The Brainly Com




Draw The Graphs Of Following Quadratic Functions I Y X 2




Graphing A Parabola Of The Form Y X 2 Bx C Practice Algebra Practice Problems Study Com



View Question The Graph Of The Parabola Defined By The Equation Y X 2 2 3 Is Rotated 180 Degrees About Its Vertex Then Shifted 3 Units To The Left T




Quadratic Systems A Line And A Parabola Video Khan Academy




How To Draw Y 2 X 2



The Parabola Below Is A Graph Of The Equation Y X 1 2 3 Mathskey Com



Quadratics Graphing Parabolas Sparknotes
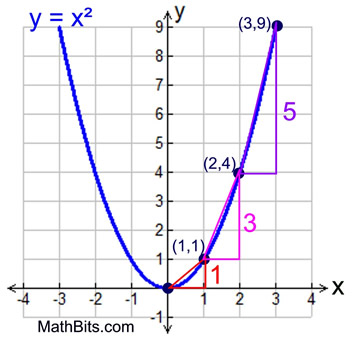



Quadratic Function Rate Of Change Mathbitsnotebook A1 Ccss Math



Solution The Parabola Y X 2 3 Intersects The X Axis At Two Points P And Q What Is The Distance From P To Q




Step To Draw Y X 2 4x 1and Find Solution To Quadratic Equation Y X 2 5x 4 Youtube



Solution Y X2 2x 3 And How Do You Graph It
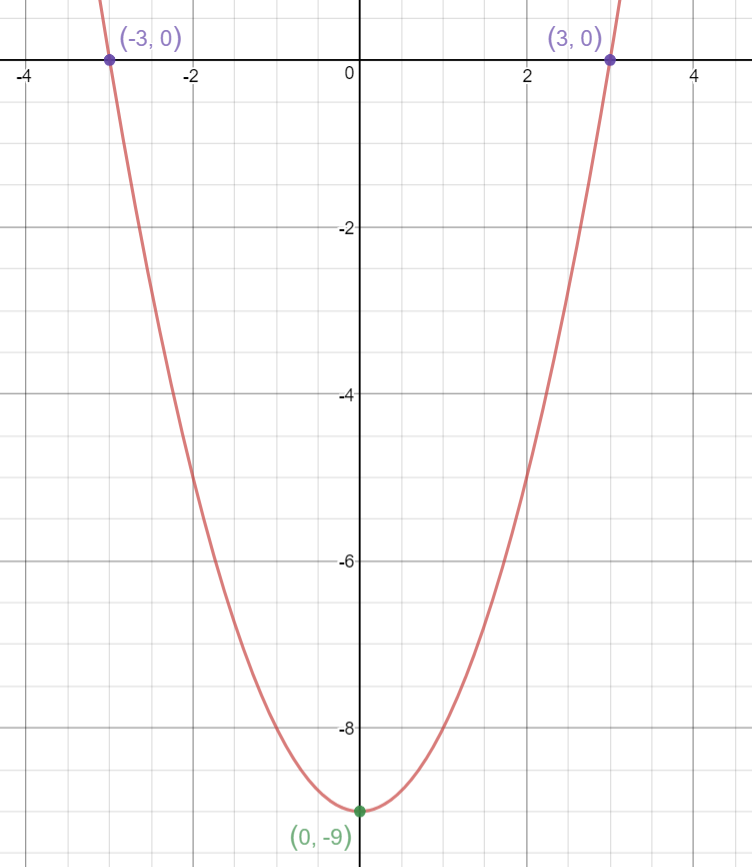



How Do You Graph Y X 2 9 Socratic



Graphing Quadratic Functions
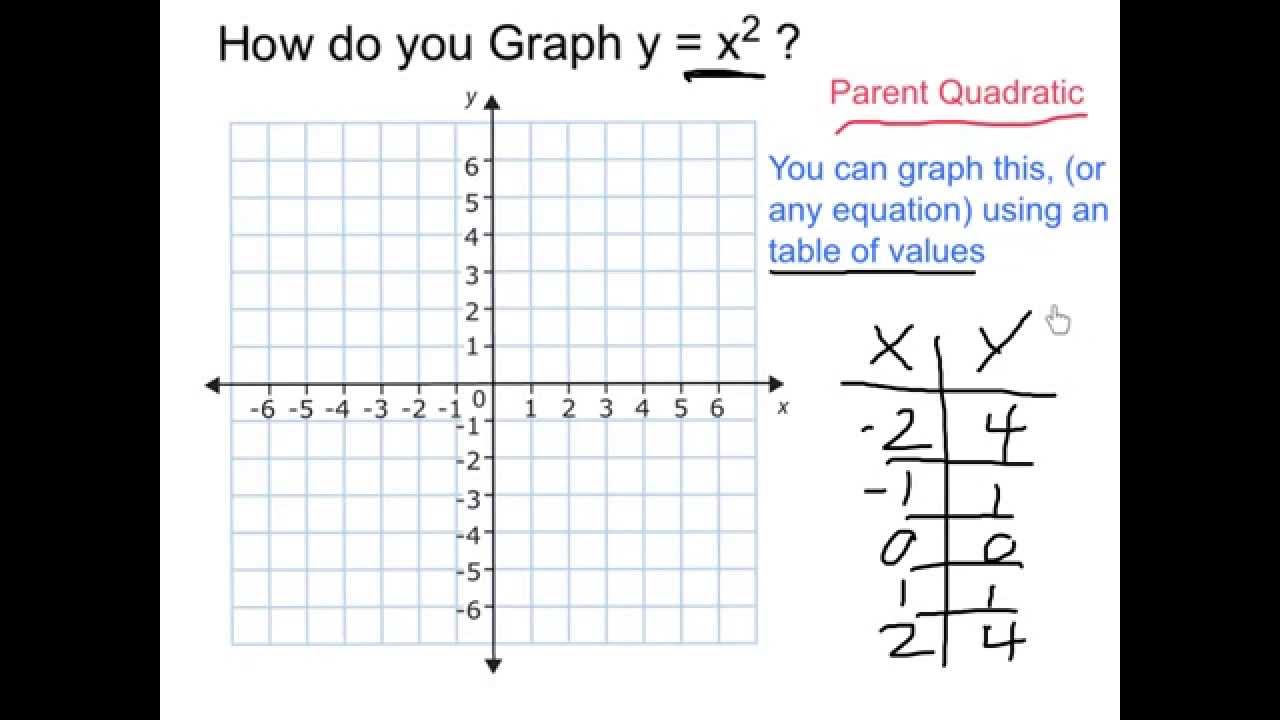



Graph Y X 2 Youtube




Geometric Solution Of X X 3 9 36 As The Intersection Of The Download Scientific Diagram



Quadratics Graphing Parabolas Sparknotes



Quadratic Functions




5 2 Properties Of Parabolas Ppt Video Online Download




Graph Y X 2 3 Youtube



Solution Find The Coordinates Of The Points Of Intersection Of The Parabola Y X2 And The Line Y X 2



0 件のコメント:
コメントを投稿